Spatial functions

Overview

Many of the of the Spatial functions require arguments of type Spatial. Data Management's Spatial data type supports the processing of spatial information, including points and polygons. The Spatial Input and Spatial Join tools operate on spatial data, as do a number of spatial functions.

Fields containing spatial data are of type Spatial. A datum of type Spatial may contain one of the following:

Point: An (X,Y) coordinate pair. Coordinates must be latitude/longitude degrees, where X=longitude, and Y=latitude. Latitude is in the range [-90...90] and longitude is in the range [-180...180].)
MultiPoint: A collection of one or more points.
LineSegment: A straight line with two endpoints.
Polyline: A collection of line segments, arranged as multiple connected groups.
Ring: A closed sequence of points defining a shape.
Polygon: A shape created by "connecting the dots" of a set of points.
Rectangle.
Null.
Error.

You can use the Calculate tool to create a new field to hold spatial data.

Shapes that span the date-line (for example, Aleutian Islands or Wangel Island) are handled properly. A geographical projection is applied before any operations that require area or distance computation.

Area

Returns the area of a polygon.

Syntax

Area( polygon)

The required argument polygon must describe a polygon and be of type Spatial.

BoundingRect

Returns a Spatial value that is the bounding rectangle of polygon.

Syntax

BoundingRect( polygon )

The required argument polygon must describe a polygon and be of type Spatial.

Centroid

Returns a Point which is the centroid of a Polygon.

Syntax

Centroid( polygon )

The required argument polygon must describe a polygon and be of type Spatial.

Remarks

This function computes the centroid of a polygon by treating the polygon as a solid two-dimensional object, and computing the "center of mass" of the object.

If the argument polygon is not a Polygon, an Error value will be returned.

The result of this function is a Point. Points are stored using a type Spatial. You can extract the X and Y coordinates of a Point using the PointX and PointY functions.

Example

Centroid(POLYGON)

Compose

Composes similar shape types by simple combination of coordinates, resulting in a multi-part shape

Syntax

Compose( shape1, shape2 )

The required arguments shape1 and shape2 must be of type Spatial.

Remarks

The following table indicates which shape types can be composed, and the resulting type:

Shape type	Point	MultiPoint	LineSegment	Polyline	Rect	Polygon
Point	MultiPoint	MultiPoint	invalid	invalid	invalid	invalid
MultiPoint	MultiPoint	MultiPoint	invalid	invalid	invalid	invalid
LineSegment	invalid	invalid	Polyline	Polyline	invalid	invalid
Polyline	invalid	invalid	Polyline	Polyline	invalid	invalid
Rect	invalid	invalid	invalid	invalid	Polygon	Polygon
Polygon	invalid	invalid	invalid	invalid	Polygon	Polygon

ConvexHull

Calculates the smallest-area polygon that completely encloses all of the points or vertices of shape.

Syntax

ConvexHull( shape )

The required argument shape must be of type Spatial.

Remarks

This function calculates the smallest-area polygon that completely encloses all of the points or vertices of the shape. This polygon is often simpler (contains fewer vertices) than the original polygon. A good visualization of the convex hull is to think of an infinitely stretchy rubber band that is stretched around the shape and then allowed to shrink as far as possible while still containing the original shape.

CountParts

Returns the number of component shapes within the given shape.

Syntax

CountParts( shape )

The required argument shape1 must of type Spatial.

Remarks

This function returns the number of component shapes within the given shape, as follows:

Polygon: the number of sub-polygons or "rings".
Polyline: the number of disconnected polylines.
Multipoint: the number of points.
Point: 1
Rectangle: 1
Linesegment: 1

See also related function Compose, and related tools Spatial Summarize and Spatial Decompose.

Cut

Subtracts the area of shape1 from shape2.

Syntax

Cut( shape1, shape2 )

The required arguments shape1 and shape2 must of type Spatial, and shape2 must be a polygon.

Remarks

The Spatial value shape1 may be of any Spatial type. For example, if shape1 is a polyline, the function removes the parts of the line segments that fall within shape2. If shape1 is a multipoint, the function removes the points that fall within shape2.

Example

Start with a polygon containing the outline of the state of Florida and an arbitrary circle (shown here in ESRI ArcGIS Explorer):

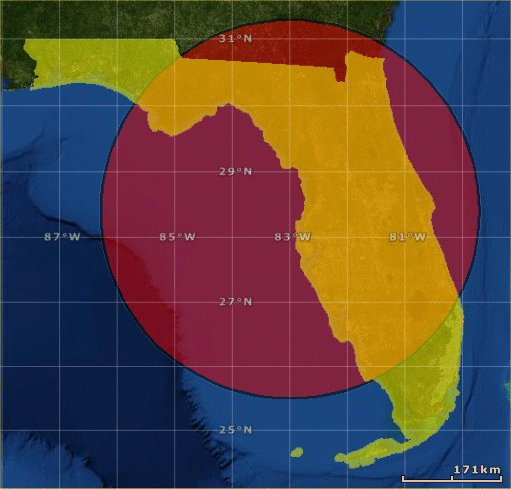
Cutting the circle from the state of Florida outline results in this shapefile:

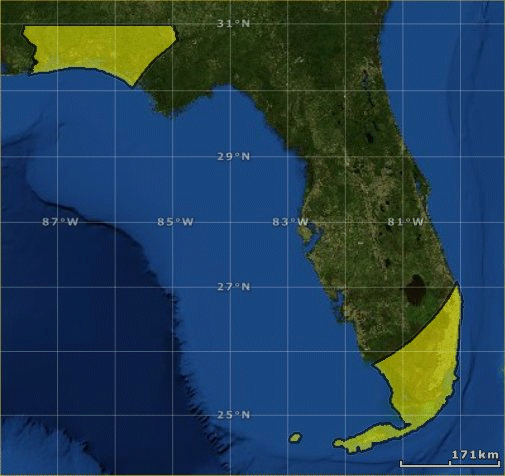
Deflate

Decreases the size of a polygon.

Syntax

Deflate( polygon, unit, amount )

The Deflate function syntax has the following arguments:

Part

Description

polygon

Required. Must describe a polygon and be of type Spatial.

unit

Required. Literal string specifying unit of measurement for amount. Must be one of:

MI (miles)
KM (kilometers)
FT (feet)
M (meters)

amount

Required. Amount by which to trim the polygon perimeter.

Remarks

This function trims the perimeter of the polygon by the defined amount, reducing its size uniformly.

FixPolygon

Corrects polygon ring orientation.

Syntax

FixPolygon( polygon )

The FixPolygon function returns a new polygon whose interior rings are oriented counter-clockwise, and whose exterior rings are oriented clockwise. This is the convention used by most geospatial software. You may need to use this if you have used the Spatial Process tool to create polygons from points, or if you have composed multiple polygon rings without ensuring the correct orientation.

The behavior of polygons with intersecting rings is undefined, as the function cannot determine which should are interior and which are exterior.

Remarks

A polygon shape may contain more than one closed ring of points. Non-overlapping rings denote disjoint parts of the polygon, like the Hawaiian islands. Rings that are enclosed in other rings are “holes”, like lakes on land.

GreatCircleDistance

Computes the "Great Circle Distance" between two geographical points.

Syntax

GreatCircleDistance( lat1, lon, lat2, lon2, unit )

The GreatCircleDistance function syntax has the following arguments:

Part	Description
lat1	Required. Numeric latitude of first point in degrees (NAD datum).
lon1	Required. Numeric longitude of first point in degrees (NAD datum).
lat2	Required. Numeric latitude of second point in degrees (NAD datum).
lon2	Required. Numeric longitude of second point in degrees (NAD datum).
unit	Required. Literal string specifying unit of measurement for returned result. Must be one of: MI (miles) KM (kilometers) FT (feet) M (meters)

Remarks

This function calculates the shortest distance over the earth's surface between two points.

InflateRound

Increases the size of a polygon, producing rounded corners.

Syntax

InflateRound( shape, unit, amount )

The InflateRound function syntax has the following arguments:

Part	Description
shape	Required. Must describe a polygon and be of type Spatial.
unit	Required. Literal string specifying unit of measurement for amount. Must be one of: MI (miles) KM (kilometers) FT (feet) M (meters)
amount	Required. Amount by which to trim the polygon perimeter.
npoints	Required. The number of points used to approximate the continuous curve of the rounded corner. Must be an Integer >4 and <1000.

Remarks

This function adds the defined amount to the perimeter of the polygon, increasing its size uniformly. At corners, produces rounded ends, using npoints points to approximate circle arcs.

InflateSquare

Increases the size of a polygon, producing square corners.

Syntax

InflateSquare( shape, unit, amount )

The InflateSquare function syntax has the following arguments:

Part

Description

shape

Required. Must describe a polygon and be of type Spatial.

unit

Required. Literal string specifying unit of measurement for amount. Must be one of:

MI (miles)
KM (kilometers)
FT (feet)
M (meters)

amount

Required. Amount by which to trim the polygon perimeter.

Remarks

This function adds the defined amount to the perimeter of the polygon, increasing its size uniformly. At corners, produces square ends.

Intersect

Intersects two polygons, returning a new polygon that contains only the overlapping area of the two.

Syntax

Intersect( polygon1, polygon2 )

The required arguments polygon1 and polygon2 must describe polygons and be of type Spatial.

Example

Start with a polygon containing the outline of the state of Florida and an arbitrary circle (shown here in ESRI ArcGIS Explorer):

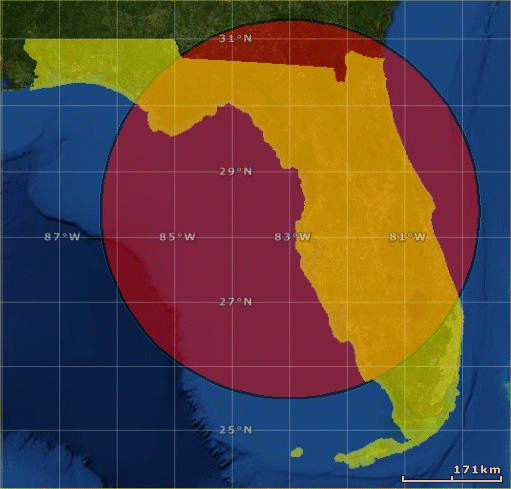
Intersecting the circle and the state of Florida outline results in this shapefile:

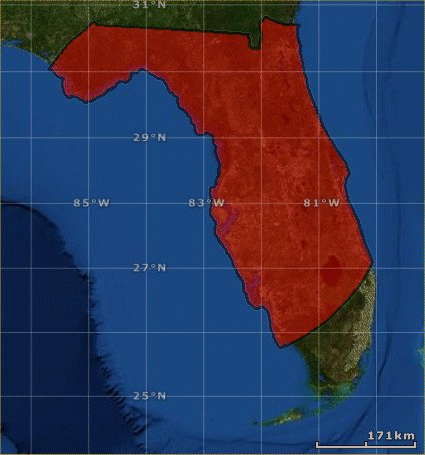
IsLineSegment

Tests whether a shape is a line segment.

Syntax

IsLineSegment( shape )

The required argument shape must be of type Spatial.

Remarks

This function returns True if the given spatial object shape is a line segment.

IsMultiPoint

Tests whether a shape is a collection of points.

Syntax

IsMultiPoint( shape )

The required argument shape must be of type Spatial.

Remarks

This function returns True if the given spatial object shape is a collection of points.

IsPoint

Tests whether a shape is a point.

Syntax

IsPoint( shape )

The required argument shape must be of type Spatial.

Remarks

This function returns True if the given spatial object shape is a point.

Example

IsPoint(MakePoint(40.2, -105.3)) returns True.

IsPolygon

Tests whether a shape is a polygon.

Syntax

IsPolygon( shape )

The required argument shape must be of type Spatial.

Remarks

This function returns True if the given spatial object shape is a polygon.

Example

IsPolygon(SPATIAL_FIELD)

IsPolyline

Tests whether a shape is a polyline.

Syntax

IsPolyline( shape )

The required argument shape must be of type Spatial.

Remarks

This function returns True if the given spatial object shape is a polyline.

Example

IsPolygon(SPATIAL_FIELD)

MakeCircle

Returns a circle constructed from coordinates and the specified radius.

Syntax

MakeCircle( lat, lon, unit, radius, npoints )

The MakeCircle function syntax has the following arguments:

Part	Description
lat	Required. Numeric latitude of center point in degrees (NAD datum).
lon	Required. Numeric longitude of center point in degrees (NAD datum).
unit	Required. Literal string specifying unit of measurement. Must be one of: MI (miles) KM (kilometers) FT (feet) M (meters)
radius	Required. Numeric
npoints	Required. The number of points used to approximate the continuous curve of the circle. Must be an Integer 4-1000 (inclusive).

MakeLineSegment

Creates a line-segment spatial object and returns it.

Syntax

MakeLineSegment( x1, y1, x2, y2, )

The MakeLineSegment function syntax has the following arguments:

Part	Description
x1	Required. X component (typically longitude) for start of line.
y1	Required. Y component (typically latitude) for start of line.
x2	Required. X component (typically longitude) for end of line.
y2	Required. Y component (typically latitude) for end of line.

All arguments must be numeric.

Remarks

The MakeLineSegment function accepts the X and Y components of two coordinate pairs and produces a Line. The returned value is of type Spatial.

Example

MakeLineSegment(40.2, -105.3, 40.5, -105.28)

MakePoint

Returns a point constructed from coordinates.

Syntax

MakePoint( x, y )

The MakePoint function syntax has the following arguments:

Part	Description
x	Required. X component (typically longitude).
y	Required. Y component (typically latitude).

Both the X and Y arguments must be numeric.

Remarks

The MakePoint function accepts the X and Y components of a coordinate and produces a Point. The returned value is of type Spatial.

Example

MakePoint(40.2, -105.3)

MakeRect

Returns arRectangle constructed from coordinates.

Syntax

MakeRect( left, bottom, right, top )

The MakeRect function syntax has the following arguments:

Part	Description
left	Required.
bottom	Required.
right	Required.
top	Required.

All arguments must be numeric.

Remarks

The MakeRect function accepts the X and Y components of a rectangle and produces a Rectangle. The returned value is of type Spatial.

Example

MakeRect(0.0, 0.0, 1.0, 1.0)

PointInPolygon

Returns a Boolean value, which is True if the point argument is physically in the polygon argument, otherwise False.

Syntax

PointInPolygon( polygon, point )

The PointInPolygon function syntax has the following arguments:

Part	Description
polygon	Required. Must describe a polygon and be of type Spatial.
point	Required. Must describe a point and be of type Spatial.

Example

IF PointInPolygon([SpatialPolygon], MakePoint([LONG], [LAT])) THEN 0 ELSE ReturnValue ENDIF

PointX

Returns the X coordinate of a point.

Syntax

PointX( point )

The required argument point must describe a point and be of type Spatial.

Remarks

This function extracts the X coordinate of a point and returns it as a floating-point number.

If the argument point is not a point, an Error value will be returned.

Example

PointX(Centroid(POLYGON))

PointY

Returns the Y coordinate of a point.

Syntax

PointY( point )

The required argument point must describe a point and be of type Spatial.

Remarks

This function extracts the Y coordinate of a point and returns it as a floating-point number.

If the argument point is not a point, an Error value will be returned.

Example

PointY(Centroid(POLYGON))

PolygonContains

Returns true if the polygon completely contains the shape. Shape may be any spatial object.

Syntax

PolygonContains( polygon, shape )

PolygonOrientation

Returns a text string describing the orientation of a polygon.

Syntax

PolygonOrientation( polygon )

The PolygonOrientation returns one of the following:

Text	Description
clockwise	All rings of the polygon are clockwise.
counterclockwise	All rings of the polygon are counter-clockwise.
both	Some rings are clockwise and some are counter-clockwise.
error	Input is not a polygon.

RectToPolygon

Converts a rectangle to a polygon.

Syntax

RectToPolygon( rectangle )

The required argument rectangle must describe a rectangle and be of type Spatial.

Remarks

This function converts a rectangle to the equivalent polygon. This is useful because some operations such as the Centroid function and the Spatial Join tool accept polygons but not rectangles.

The result of this function is a Polygon. Polygons are stored using a type Spatial.

Example

RectToPolygon(MakeRect(0.0, 0.0, 1.0, 1.0))

ShapesIntersect

Returns true if the edges of two shapes intersect each other.

Syntax

ShapesIntersect( shape1, shape2 )

The required arguments shape1 and shape2 must be a rectangle, polygon, line, or polyline of type Spatial.

SpatialType

Reads a spatial value (shape) and returns the spatial type of the shape.

Syntax

SpatialType( shape )

The required argument shape must be of type Spatial.

Remarks

The return value is one of the following text strings:

Invalid
Point
LineSegment
Rectangle
Polygon
Polyline
MultiPoint

Union

Union two polygons.

Syntax

Union( polygon1, polygon2 )

Remarks

Unites the two polygons, returning a new polygon that contains all area covered by either polygon.